(Cubic Hermite Spline's derivative on an arbitrary interval)
최근에 일하다가 오랜만에 Hermite 스플라인을 건드릴 일이 있어서 간단 정리.
1. Hermite Spline 구하기
1.1. 제약조건 4가지
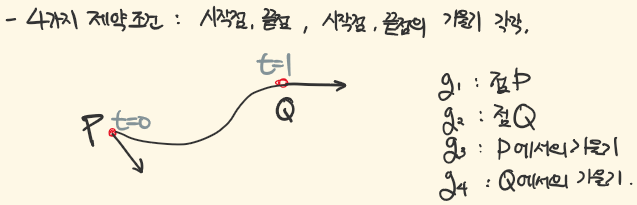
cubic (3차) 함수로 표현되니, 4개의 제약조건을 가질 수 있다. Hermite Spline은 시작점, 끝점의 위치와 속력(=기울기)를 사용함.
위에서 나열한 순서와는 다르게, 보통 g2와 g3을 바꿔 (위치, 속력, 위치, 속력) 순서로 쓰는데 (이러면 더 알아보기 쉽다) 예전에 노트에 정리해 둘때는 (위치 위치 속력 속력) 으로 정리해두는 바람에 그냥 이대로 진행함.
1.2. Blending functions 구하기
구하고자 하는 Hermite spline, X(t).
$$X(t)=T\cdot A$$
$$T=\begin{bmatrix}
t^{3} & t^{2} & t & 1
\end{bmatrix}$$

$$즉, G=B\cdot A 이고$$
$$ A=B^{-1}\cdot G $$
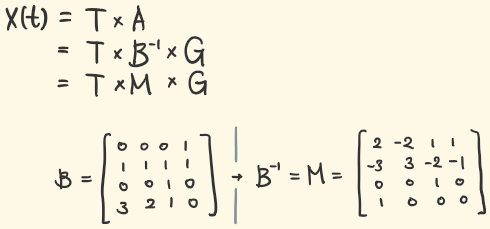
B의 역행렬을 구해서 T와 곱해 방정식의 형태로 늘여써주면, 아래처럼 정리할 수 있다. 각 파라메터 (g1, g2..) 앞에 붙은 cubic 함수가 blending functions.
(역행렬을 구할 땐 https://matrix.reshish.com/inverse.php가 편하다)
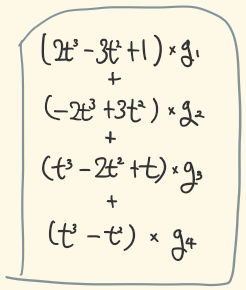
2. On an arbitrary interval [x_{k+1}, x_k]
위에서 구한 Hermite spline은 t가 [0, 1] 구간에만 유효하다.
- t = 0 일 때 (위치:g1, 속력:g3)이고,
- t = 1일 때 (위치: g2, 속력: g4)를 찍고
그 이전, 이후 구간에서는 의도된 세팅과는 전혀 관계없는 이상한 값이 나올 것이란 이야기.
하지만, t를 임의의 구간으로 설정하고 싶을 때가 있다. 예를 들어 t가 [3, 5] 구간에 있을 때에 대해 원하는 위치와 속력으로 값을 보간하고 싶다면?
이때 그냥 't를 해당 interval의 길이로 정규화시키면 되지 않을까'라고 생각할 수 있는데, 안된다.
예를 들어 시작점 (위치:1, 속력:1) / 끝점 (위치:0.7, 속력:0)의 설정으로 Hermite spline을 구한다고 해보자.


t를 아래처럼 정규화해서 넣어주면 오른쪽에서의 까만색 그래프가 그려진다. 이는 왼쪽 주황색 그래프를 ([0, 1] 구간) 목표 interval의 길이만큼 강제로 좌우로 늘려버린 모양새가 된다.
$$ t_{normalized} = (t - 3) / (5 - 3) $$
이렇게 그래프를 그냥 좌우로 늘려버리면 그에 따라 그래프의 기울기(=속력)도 당연히 같이 늘려지게 된다. 파라미터 설정한 속력과는 다른 spline이 세팅 되는것이니 이는 틀린 답임.
우리가 원하는 건 기울기가 유지되는 초록색 그래프. 이렇게 만들려면 좌우로 그래프를 늘려주는 만큼 줄어드는 속력을 compensate 해줘야 한다. 그러기 위해선 구간의 길이만큼 속력을 곱해서 늘려주면 된다.
아래와 같은 임의의 구간에서의 스플라인 곡선 P(x)는 아래와 같다.
(여기선 다시 위치, 속력, 위치, 속력 순서로 바꿈)
$$interval = [x_k, x_{k+1}]$$
$$P(x)=\begin{bmatrix}
t^3 & t^2 & t & 1
\end{bmatrix}\cdot \begin{bmatrix}
2 & 1 & 2 & 1\\
-3 & -2 & 3 & -1\\
0 & 1 & 0 & 0\\
1 & 0 & 0 & 0
\end{bmatrix}\cdot \begin{bmatrix}
p_k\\
(x_{k+1}-x_k)\cdot m_k\\
p_{k+1}\\
(x_{k+1}-x_k)\cdot m_{k+1}
\end{bmatrix}$$

위키피디아 항목에서도 언급되어 있다.
이때 h00(t), h10(t).. 함수들은 위에서 언급한 blending function 들임.
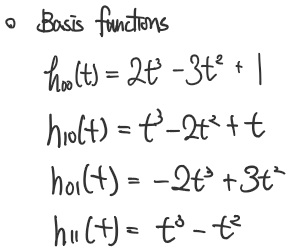
3. Derivative
작업하던 코드에서는 도함수도 계산해서 넣어줘야 했다.
임의의 구간에서 스플라인 P(x)의 도함수는 아래와 같다. 아래쪽 수식을 가져다 쓰는 게 코드에서 보기 더 편하다. blending functions를 각각 t에 대해 미분하고, 거기에 interval의 길이를 나눠주는 모양새라서 보기에 더 익숙함.
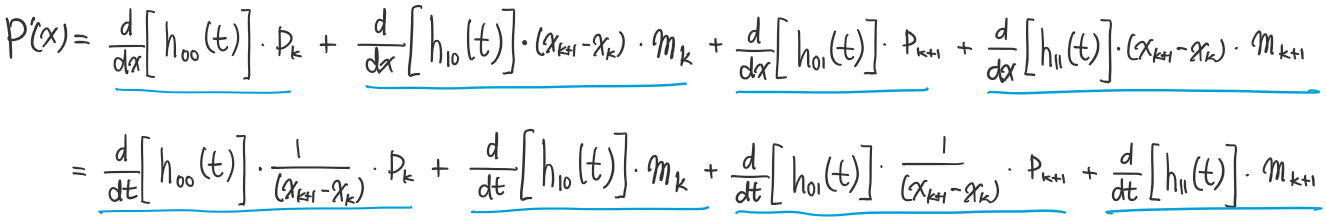
위쪽 수식을 아래쪽 수식으로 바꿔 쓸 수 있는 이유는, 아래처럼 blending functions (h00(t), h10(t)) 를 x에 대해 미분하면 각각 t에 대해 미분한 형태에 interval의 길이를 나눈 꼴이 되기 때문임.
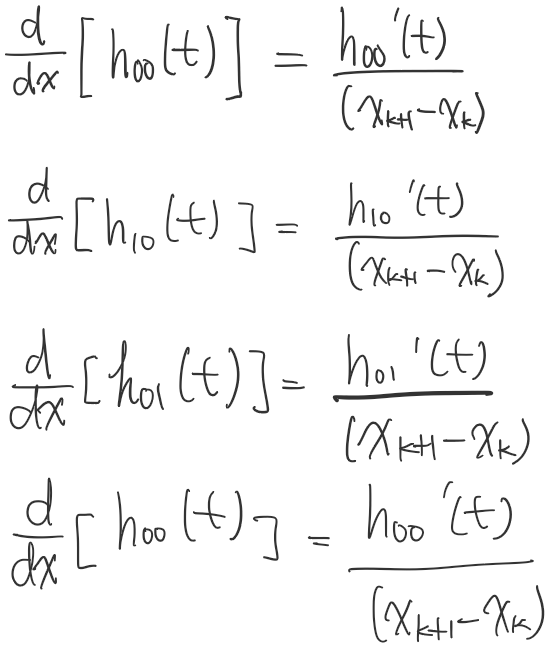

$$ \frac{d}{dx}[h_{00}(t)] = \frac{6t^2-6t}{(x_{k+1}-x_k)} = \frac{d}{dt}[h_{00}(t)] \cdot \frac{1}{(x_{k+1}-x_k)} $$
이렇게 t에 대해 미분한 형태에 interval의 길이를 나눈 꼴이 됨. 다른 blending function에 대해서도 마찬가지. 그래서 두 번째, 세 번째 항에서 interval의 길이를 곱해주던 (속력을 compensate 해주던) 부분이 사라지게 됨. 따라서 위에 언급한 대로의 수식이 나온다.

아래 desmos 링크에 적당히 parameterize 해서 건드려 볼 수 있게 만들어두었다. 확인해보시길.
'Note' 카테고리의 다른 글
| C#에서 Dictionary에 Enum을 써도 괜찮은것 같다 (1) | 2019.12.23 |
|---|---|
| TIL: 스칼라(jvm)에서 JS코드 실행하기 (0) | 2017.10.09 |
| TIL: 코루틴(Coroutine)에 대해 몇 가지 (0) | 2017.07.10 |
| TIL: C#에서 enum이나 struct를 Dictionary의 Key값으로 사용하면 쓰레기가 생긴다 (1) | 2017.07.06 |
| TIL: docker 컨테이너안에서 ip 바인딩은 localhost가 아니라 0.0.0.0으로 해야한다 (0) | 2017.07.02 |