EDIT 2023-02-16: 개요에서 불필요한 부분 삭제 및 정리. 아래 오일러 각, 짐벌락 내용 추가.
0. 개요
3D 공간에서 회전, 방향을 표현하는 방식에는 여러가지가 있다. 많이 쓰이던 방식으로 오일러(Euler) 각을 통한 표현법이 있고, 오일러각에서 발생할 수 밖에 없는 짐벌락(Gimbal Lock) 문제를 해결하기 위해 요즘은 쿼터니온을 많이 사용한다. 이것들에 대해서 정리 해보도록 한다.
1. 정의
복소수처럼 실수부와 허수부의 조합으로 이루어짐. 대신 사원수는 허수 \(i,j,k\)의 3개를 사용한다. 이 허수들 사이에는 다음과 같은 관계가 성립한다.
$$i^2 = j^2 = k^2 = ijk = -1$$
여기서 중요한 점은 곱셈의 교환법칙이 성립하지 않는다는점. 위의 식을 정리해보면 \(k = ij = -ji\)로, 곱셈 순서에 따라 결과값도 달라진다.
이런 세 허수들\((i,j,k)\)과, 네 개의 실수들\((w,x,y,z)\)으로 이루어진 사원수는 다음과 같다. $$q = w + xi + yj + zk$$
앞의 계수들만 모아서 아래처럼 쓰기도 한다. $$q = (w,x,y,z)$$
또는 허수부에 붙는 계수들을 하나의 벡터로 몰아서 아래처럼 쓰기도 한다. (\(v = (x,y,z)\)) $$q = (w,v)$$
2. 연산
2.1. 덧셈
덧셈은 그냥 하던대로 항 맞춰서 더하면 된다.
2.2. 곱셈
삼원수가 곱셈에 대해 닫혀있지 않았지만, 사원수는 곱셈에 대해 닫혀 있다. (사원수끼리 곱하면 사원수가 나옴)
곱셈도 그냥 하던대로 항 맞춰서 전개하면 되지만, 실수부가 0인 사원수 두 개를 곱해서 나온 식을 정리해 보면 벡터의 내,외적 연산으로 나타낼 수 있음을 알 수 있다. 그 다음으로 실수부에 미지수를 하나 두고 전개해 본 다음, 아까 했던것 처럼 벡터 연산 부분만 모아보면 아래 처럼 식이 정리된다.
$$q_1 \cdot q_2 = (w_1w_2 - (v_1 \cdot v_2), w_1v_2 + w_2v_1 + (v_1 \times v_2))$$
2.3. 켤레 (Conjugate)
복소수와 비슷하게 허수부의 부호만 바꿔준다
$$q = (w,v)$$ $$q^* = (w,-v)$$
이때 다음과 같은 성질들을 만족한다.
$$(q^*)^* = q$$ $$(pq)^* = q^*p^*$$ $$qq^* = q^*q$$
2.4. 크기 (Norm)
계수들로 이루어진 4차원 벡터 길이를 구하는것과 같다.
$$\lVert q \rVert = \sqrt{qq^*} = \sqrt{q^*q} = \sqrt{w^2+x^2+y^2+z^2}$$
이것도 마찬가지로 사원수 하나와 그 켤레를 곱하는 식을 (\(qq^*\)) 정리해보면 계수들의 제곱의 합 꼴로 정리된다.
2.5. 항등원과 역원 (Identity & Inverse)
항등원은 다음과 같다. $$I = (1,0,0,0)$$ $$q \cdot I = I \cdot q = q$$
역원은 다음과 같다. $$q^{-1} = \frac{q^*}{\lVert q \rVert^2}$$ $$q \cdot q^{-1} = q^{-1} \cdot q = I$$
위에서 Norm 계산할 때 언급했던것 처럼 \(qq^*\)를 계산해 보면 4차원 벡터의 길이에 루트 안 씌운꼴이 된다. 그래서 길이 제곱을 나눠주는것이고.
3. 회전
3.0. w,x,y,z값
임의의 단위벡터 \(\hat{v}(x,y,z)\)축을 기준으로 \(2\theta\)만큼 (\(\theta\)가 아니다) 회전하는 회전 변환을 사원수로 나타냈을때, \(w,x,y,z\)값은 다음과 같다.
$$ w = cos\theta $$ $$ x = sin\theta \cdot x_v $$ $$ y = sin\theta \cdot y_v $$ $$ z = sin\theta \cdot z_v $$
왜 \(\theta\)가 아니라 \(2\theta\)냐면, 사원수의 회전 변환을 적용시키는 식에서 우리가 원하는 차원의 공간만을 등복각(isoclinic) 회전 시켜주기 위해서, 사원수를 두 번 곱해주기 때문.
3.1. 허수, 복소수
중학교때 배웠던것 처럼, 복소수는 복소평면이라는 2차원 평면위의 점을 표현하는 용도로 사용할 수 있다. \(a+bi\)에서 \(a\)를 마치 \(x\)값처럼, \(b\)를 마치 \(y\)축의 값 처럼 바라보겠다는 것이다. 잘 생각해보자. 수학시간에 허수를 배우기 전까지 배웠던 모든 수들, 그러니까 실수는 하나의 수직선(축) 위에 나타낼 수 있었다. 자연수, 0, 음수, 무리수 전부. 하지만 허수는 수직선의 어디에도 있을 곳이 없다. 그렇기 때문에 수직선의 바깥으로, 원점에서 위의 방향으로 하나의 수직선을 더 그어서(한 차원을 더 늘려서) 허수가 존재하는 축을 만든것이다.
여기까진 알겠는데 생각해보면 \(xy\) 좌표평면이랑 다를게 없다. 어차피 복소수의 2개의 차원값으로 복소평면위의 한 점을 나타낼 수 있는것, 복소수들을 더하고 빼면서 점을 이동시키는것은 원래 그냥 좌표계에서도 다 해왔던것들이니까. 그냥 \(i\)라는 글자만 쓰는것 이외에 다를게 없다.
하지만 \(i\)를 쓰면서 중요한 차이점이 하나 생기는데, 바로 허수 \(i\)를 두 번 곱하면 -1이 된다 는것이다. 조금 더 설명을 더해서 다시 말하자면, 1에 \(i\)를 네번 곱해야 다시 1로 되돌아 온다는것이다. 한번만 더 설명을 더 해서 다시 말하면, 허수 \(i\)의 곱셈은 '시계 반대 방향의 90° 회전' 시키는것과 같다.
숫자 1을 복소평면 위에 놓고 \(i\)를 계속 곱해보자.
- \(1\)을 복소평면위의 점으로 표현하자면 \((1,0)\)이다. $$1 \rightarrow (1,0)$$
- \(1\)에 \(i\)를 곱하면 실수부는 사라지고 허수 \(i\)만 남는다. 이는 복소 평면에서 \((0,1)\)로 나타낼 수 있고, 기존의 \((1,0)\)을 반시계방향으로 90° 회전한것과 같은 의미를 가진다. $$1 \cdot i = i \rightarrow (0,1)$$
- \(i\)에 다시 \(i\)를 곱하면 -1이 된다. 여전히 90° 회전한 것과 같이 허수부가 사라지고 실수부만 남는다. $$i \cdot i = i^2 = -1 \rightarrow (-1,0)$$
- 마찬가지로 다시 \(-i\)가 된다. $$-1 \cdot i = -i \rightarrow (0,-1)$$
- 마지막으로 \(i\)를 곱하면서 시작점으로 되돌아온다. $$-i \cdot i = -i^2 = 1 \rightarrow (1,0)$$
혼자 연습장 펴놓고 \((1,1)\) 점에 \(i\)를 네번 곱해가면서 점들의 위치가 어떻게 변해가는지, \(i\)들이 어떻게 곱해지는지 한번 해보시길.
3.2. 복소수의 곱셈
위에서 허수의 곱셈이 90°회전을 의미하는것처럼, 복소수를 곱하는 것도 일정 각도만큼 반시계 방향으로 회전하는것을 의미한다. 조금 다르게 말하자면, (2차원) 회전 변환을 복소수로 표현할 수 있고, 이 복소수들의 곱셈으로 회전 변환을 수행할 수 있다.
예를들어, 복소평면 위에 두 점\((1 + i), (1 + \sqrt{3}i)\)이 있다고 생각해보자.
- 이 두 점들을 각각 극좌표계로 나타내자면 \((\sqrt{2}, 45^{\circ}), (2, 60^{\circ})\)이다.
- 두 복소수를 곱한 \((1 + i) \times (1 + \sqrt{3}i)\)를 풀어서 정리하면 \((1-\sqrt{3}) + (1+\sqrt{3})i\)가 된다.
- 2.에서 나온 결과를 극좌표계로 나타내면 \((2 \sqrt{2}, 105^{\circ})\)로, 1.에서 보인 두 극좌표계 점의 길이를 곱하고, 각도를 더한 값과 같다.
즉, 복소수의 곱셈은 극좌표계로 봤을때의 길이(원점과의 거리)를 곱하고, 각도를 더하는 행위와 같다. $$(r_1, \theta_1) \times (r_2, \theta_2) = (r_1 \times r_2, \theta_1 + \theta_2)$$
그렇다면 복소평면위의 어떤 점에 대해서 우리가 적용하고자 하는 회전 변환은 다음과 같은 회전 복소수로 나타낼 수 있다.
$$(1,\theta) \rightarrow (cos\theta, sin\theta) \rightarrow cos\theta + sin\theta \cdot i$$
3.3. 오일러의 공식
오일러의 공식은 다음과 같다. $$e^{ix} = cos(x) + i \cdot sin(x)$$ 우변을 잘 보면, 극좌표계 \((1,x\))를 복소평면위의 한 점으로 변환한 것과 모양새가 같다. 때문에, \(\theta\)만큼의 회전 변환을 나타내는 회전 복소수는 \(e^{i\theta}\)로 표현할 수 있다.
3.4. 회전 사원수
복소수가 2차원 회전변환을 나타낼 수 있는것처럼, 사원수를 이용해서 4차원 회전변환을 나타낼 수 있다. 이들은 실수부\((w)\) 값이 0이고, 허수부가 단위 벡터 \(\hat{v}\)로 이루어져있다. 이렇게 크기가 1인 사원수를 단위 벡터처럼 단위 사원수라고 하며 \(\hat{r}\)로 나타낸다.
오일러의 공식을 이용하면 회전 사원수 \(e^{\hat{r}\theta}\)는 아래와 같이 나타낼 수 있다.
$$e^{\hat{r}\theta} = cos \theta + sin \theta \cdot \hat{r}$$
이때 실수부 값은 0이기 때문에,
$$e^{\hat{r}\theta} = cos \theta + sin \theta \cdot 0 + sin \theta \cdot \hat{v}$$ $$= cos \theta + sin \theta \cdot \hat{v}$$
이며, 이렇게 고쳐쓸 수 있다.
$$ = (cos\theta, sin\theta \cdot \hat{v})$$
이렇게 구한 회전 사원수로 점들을 회전시킬 수 있다. 3차원 공간 위의 어떤 한 점\((p_x, p_y, p_z)\)을 사원수로 나타낸것을 \(p_q\)라고 하고, \(\hat{v}\)축으로 \(\theta\)만큼의 회전각을 가진 회전 사원수를 \(\hat{q}\)라고 해보자.
$$\hat{q} = (cos \theta, sin \theta \cdot \hat{v})$$ $$p_q = (0, p_x, p_y, p_z)$$
이랬을 때,
$$\hat{q} \cdot p_q \cdot \hat{q}^{-1}$$
위의 식은 \(p_q\)를 \(\hat{v}\)축을 기준으로 \(2\theta\)만큼 회전시킨다.
이 식을 풀어서 정리하면 (이것도 복잡하니 연습장 놓고 해봐야함)
$$p' = (0, p+2w(v \times p) + 2(v \times (v \times p)))$$
실수부는 0이 되고, 허수부에 오일러-로드리게스 회전 공식이 나오게 된다. 즉, 위의 식이 확실히 3차원 공간에서의 회전 변환을 의미한다는 것을 알 수 있다.
NOTE: 그냥 회전 사원수(\(\hat{q}\))와 점의 위치를 나타내는 사원수(\(p_q\))를 그냥 곱하면 안되고 앞 뒤로 그냥 사원수와 켤레 사원수를 따로 곱해줘야 한다. 이는 등복각(isoclimic)회전과 관련이 있는데, 맨 위에서 언급한 책을 보거나 아니면 이 ppt를 참조하는게 좋을듯.
3.5. 회전 행렬로의 변환
회전 사원수를 사용해서 3차원 점들의 회전을 수행할 수도 있지만, 렌더링 파이프라인에 회전 변환을 적용시키기 위해선 결국엔 회전 사원수를 회전 행렬로 변환시켜야 한다.
변환식은 다음과 같다. 위에서 \(\hat{q} \cdot p_q \cdot \hat{q}^{-1}\)으로 얻은 오일러-로드리게스 회전공식을 전개한 다음, \(p\)에 대해서 하나의 행렬식으로 몰아보면 아래처럼 된다. (사실 책에서는 좀 더 깔끔한 방법을 제시해 주는데도 조금 헷갈려서 그냥 무식하게 전체전개 해버렸다. 복잡하지만 그래도 어떻게 또 잘 나온다)
$$M_q = \begin{bmatrix} 1 -2y^2 - 2z^2 & 2xy-2wz & 2xz + 2wy & 0 \\ 2xy + 2wz & 1 - 2x^2 -2z^2 & 2yz - 2wx & 0 \\ 2xz - 2wy & 2yz + 2wx & 1 -2x^2-2y^2 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$
4. 오일러 각
오일러 각은 3차원 공간에서 회전을 나타내는 다른 방법중에 하나로, X, Y, Z축을 중심으로 순서대로 회전하는 각도 3개를 사용한다.

이 세 개의 축을 기준으로 하는 회전각을 하나의 매트릭스로 조립해야 하는데, 이 때 필수적으로 이 셋 사이의 조립 순서가 생길 수 밖에 없다. X축을 기준으로 먼저 회전하고, (회전된 상태에서) Y축을 기준으로 또 회전하고, (마찬가지로 또 회전된 상태에서, Z축을 기준으로 회전하던가, 아니면 YXZ축 순서대로 하거나, ZXY축 순서대로 하거나... 등등.
(개별 축 회전 매트릭스를 조합해서 하나의 회전 매트릭스를 만들려면 아래 처럼 어떤 순서로 매트릭스를 조립 할 수 밖에 없다)
// 각 축에 대한 회전량을 radian으로 표현
float pitch = 0.2f; // X 축 회전
float yaw = 0.4f; // Y 축 회전
float roll = 0.6f; // Z 축 회전
// x, y, z 순서로 조립
XMMATRIX rotationMatrix =
XMMatrixRotationX(pitch) *
XMMatrixRotationY(yaw) *
XMMatrixRotationZ(roll);4.1 짐벌 (Gimbal)
짐벌(Gimbal) 이런 분리된 축에서의 회전을 표현할 수 있는 기계적 장치다. 예전에 자이로 스코프 팽이 장난감을 가지고 놀았다면 짐벌이 어떻게 회전을 표현 할 수 있는지 어느정도 익숙하겠지만, 조금 더 명확한 이해를 위해 추가 예시를 가져왔다. 그 옆의 '개 쩌는 고기 불판'을 참고 하시면 된다.


오일러 각 회전의 중요한 특성 중 하나는 회전축의 조립 순서에 따라 '의존성'이 생긴다는 것이다. X축 회전이 먼저 곱해지면, 이전의 회전이 뒤따르는 Y축 및 Z축 회전에도 영향을 미치게 된다. 다른 말로, 가장 바깥쪽의 짐벌을 회전시키면, 가장 안쪽의 짐벌도 함께 회전하게 된다. 즉, 각 하위 회전축의 경우, 회전축이 월드 스페이스에 고정되어 있지 않으며, 상위 회전축이 움직이면 그에 따라 하위 회전축도 함께 회전하게 된다.
4.1 짐벌 락 (Gimbal Lock)
하위 회전축이 돌아가다가 상위 회전축과 정렬되는 경우, 회전 할 수 있는 축이 하나 사라지는 효과를 낳게 된다. 짐벌 하나가 '잠기기' 때문에 Gimbal Lock 이라고 이야기한다. 어떤 현상인지 위키피디아에서 훔쳐온 예제를 가지고 살펴보자.
3D 편집 프로그램에서 흔히 보는 '회전 핸들'이 아니라 '짐벌'이라 은근 헷갈리는데, '링'이 얼마나 회전 되어 있는지는 전혀 신경쓰지 않아도 된다. 대신 비행기를 관통하는 '회전 중심 축'이 어딜 향해 있는지 봐야 한다. 회전 중심 축으로부터 비행기를 뚫고 지나가는 가상의 '꼬챙이'를 상상해보도록 하자.
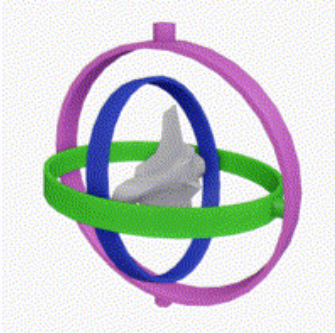
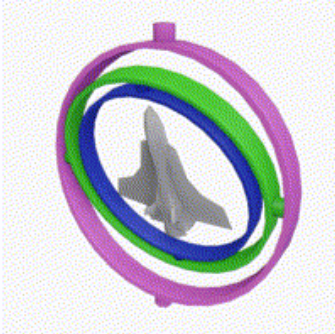

1. 3축 기준 회전축이 전부 다른 방향을 향하고 있다. 3축 회전 가능
2. '링'이 겹쳐져 있어 보이지만 사실 별 의미 없다. 파란색, 초록색, 마젠타색 짐벌의 회전 중심 축이 겹치지 않았음. 3축 회전 가능
3. 파란색 짐벌과 마젠타색 짐벌의 회전 중심축이 정렬되어 있다. 이 때 비행기가 Roll을 하거나, Yaw를 하면, 같은 중심축 기준으로 회전을 하게 된다. 월드 스페이스 기준으로 회전 할 수 있는 중심 축이 하나 잠겨서(Lock) 사라진 것과 마찬가지.

4.2. 왜 쿼터니온은 괜찮지?
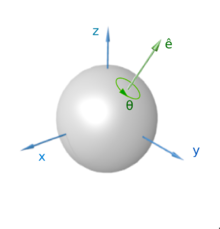
그럼 쿼터니온은 왜 이런 문제가 없는가? 하면 쿼터니온은 임의의 축 기준으로 회전을 표현 할 수 있기 때문이다. 즉, 오일러 각 처럼 x, y, z 축 마다 나누고 합치고, 합칠때 조립 순서를 따지는 일을 하지 않기 때문에, 의존성이 생기지 않음. 그래서 짐벌락 문제가 없다.
(다르게 말하자면, 쿼터니온을 써도 각 회전축마다 회전을 나눠서 하고, 다시 조립하면 짐벌락 문제가 생긴다)
References
'프로그래밍' 카테고리의 다른 글
| C#: object => IEnumerable<object> (0) | 2017.11.21 |
|---|---|
| Using Linq in Unity3d (0) | 2017.10.29 |
| 렌더링 파이프라인에서 왜 동차 좌표계를 쓸까 (4) | 2017.07.09 |
| SAT(Separating Axis Theorem) 충돌처리 구현 (0) | 2017.06.21 |
| C#의 람다 변수 캡쳐 (0) | 2017.05.29 |