아마 고2 때였을거다. 당시에는 디씨 프로그래밍갤을 종종 눈팅 하곤 했었다. 당시 자주 돌아다닌 비슷한 떡밥으로는 '1부터 100까지 더하기'나 '별찍기' 따위가 있었는데, 이때 프갤러들은 이런 문제들을 각자 웃기거나, 변태같은 방식으로 풀고 자랑하며 놀곤 했다. (제목을 '1 부터 100까지 더하는 획기적인 알고리즘' 이라고 해놓고 내용에는 printf("5050\n"); 을 적어 놓는다거나 하는)
어느날 프갤에 달팽이 문제 떡밥이 돌아다녔었다. 달팽이 문제도 1-100이나 별찍기와 마찬가지로, 프로그래밍을 처음 배우는 사람이 기초적인 문법까지 보고나서 풀어보는 간단한 응용한 문제중에 하나인데, N by N 2차원 배열에 달팽이 집 모양 처럼 나선 모양대로 정수값을 채워넣는 문제이다. 예를 들면 이런식으로.
그림1. N=5일때의 달팽이 배열.
달팽이 문제를 푸는데 당연히 여러 방법이 있겠지만, 대개는 1부터 N^2 까지 차례로 왼쪽, 아래쪽, 오른쪽, 위쪽을 순서로 돌아가면서 배열에 값을 하나씩 집어넣는 방식으로 풀곤 한다. 아무튼 프갤러들이 코드로 드립치는걸 구경하다가 어떤 링크를 보게 되었는데. 거기에선 달팽이 문제를 이렇게 풀어놓았다.
그림2. 생전 듣도보도 못한 방식이었다.1
처음 보자마자 저게 진짜로 동작하는지 의심가서 확인해본 기억이 난다. 아무리 봐도 저게 도대체 무슨 식인지도 모르겠고, 어떻게 한번에 달팽이 배열 값을 얻어낼 수 있는지도 모르겠고, 어떻게 저걸 유도해 냈을지도 상상이 안 갔고, 마지막에 printf안에 들어가 있는 i/72는 왠지 모르겠지만 엄청 쿨해보이고. 어떤 원리로 저게 굴러가는지 궁금해서 좀 더 알아보고자 댓글을 보니 라그랑주 보간법을 이용한것 같다고 하더라.2 키워드를 보자마자 위키피디아에 라그랑주 보간법을 찾아봤지만, 당시 보간을 그냥 3DsMax 같은데서 키 프레임 애니메이션 할때 중간값을 찾을때나 쓰는 정도로만 이해했기 때문에 그냥 '뭔가 어렵지만 있어보이는구나' 까지 생각하고 떡밥이 식어버리면서 잊어버리게 되었다.
대학교 3학년 1학기에 선형대수 시간에 갑자기 그 문제가 생각났다. 벡터공간에 대한 기본 성질을 배우고 있었는데 왜 그게 생각났는지 모르겠다. 선형결합 이야기 하다가 보간법 생각났고 그러다가 이 문제가 떠올랐을지도 모르겠다. 아무튼, 잠깐 생각을 해보니까 x, y값(배열의 i,j값)에 대한 z값(배열 안의 값)을 구하는 함수 형태로 나타낼 수 있다는게 떠올랐다. 위의 5x5 배열을 예로 들자면 F(0,0) = 1, F(0,1) = 2 , ... F(1,0) = 16, F(1,1) = 17, ... , F(4,4) = 9 이렇게. 그리고 저 점들을 전부 지나가는 곡선을 저 보간법을 사용하면 구할 수 있을 것 같았다. 그걸 수업시간에 교과서 옆에 휘갈겨 놓고 또 다시 잊어버렸다.
함수 구하기
그러다 어제 새벽에 갑자기 이 문제가 생각나서 구현해 보기로 했다. 위에선 3차원 함수로 구상했는데, 오랜만에 다시 찾아 보니까 라그랑주 보간법은 2차원이다. 배열에 접근할때 두 개의 오프셋을 사용해서 접근하지 않고3, 어차피 메모리상에서 선형적으로 배치되니까, 하나의 오프셋을 사용해서 접근하도록 한다.4 이렇게 하면 F(x,y) = z 꼴이 아니라 F(x) = y 꼴의 함수로 구현이 가능하게 된다.5
그럼 이제 정리하자면 F(0) = 1,F(1) = 2,F(2) = 3, ... , F(5) = 16, F(6) = 17, ... , F(24) = 9 의 점들을 지나가는 함수를 라그랑주 보간법을 사용해서 구하면 된다.
그림3. 이 점들을 전부 지나가는 함수를 구해야 한다.
증명이나 정확한 설명은 위키를 참조하자. 우리가 구하고자 하는 함수 F(x)는 (아래 수식에선 L(x))
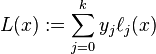 이고, 이때
이고, 이때
 이다.
이다.L(x) 함수 안에 있는 기호는 시그마이고, 이건 대부분이 알거다. l(x) 함수 안에 있는 기호는 처음 보는 경우가 있을텐데 (내가 그랬다) 이름은 파이이고 시그마가 덧셈 연산이라면 파이는 곱셈 연산이다. f=0 부터 j와 다를때 k까지에 대해 오른쪽 분수를 곱해주면 된다.
각 점들을 저 식에 대입했을때 나오는 5x5 달팽이 함수는 이렇다.
y = (x-1)/-1*(x-2)/-2*(x-3)/-3*(x-4)/-4*(x-5)/-5*(x-6)/-6*(x-7)/-7*(x-8)/-8*(x-9)/-9*(x-10)/-10*(x-11)/-11*(x-12)/-12*(x-13)/-13*(x-14)/-14*(x-15)/-15*(x-16)/-16*(x-17)/-17*(x-18)/-18*(x-19)/-19*(x-20)/-20*(x-21)/-21*(x-22)/-22*(x-23)/-23*(x-24)/-24*1+(x-0)/1*(x-2)/-1*(x-3)/-2*(x-4)/-3*(x-5)/-4*(x-6)/-5*(x-7)/-6*(x-8)/-7*(x-9)/-8*(x-10)/-9*(x-11)/-10*(x-12)/-11*(x-13)/-12*(x-14)/-13*(x-15)/-14*(x-16)/-15*(x-17)/-16*(x-18)/-17*(x-19)/-18*(x-20)/-19*(x-21)/-20*(x-22)/-21*(x-23)/-22*(x-24)/-23*2+(x-0)/2*(x-1)/1*(x-3)/-1*(x-4)/-2*(x-5)/-3*(x-6)/-4*(x-7)/-5*(x-8)/-6*(x-9)/-7*(x-10)/-8*(x-11)/-9*(x-12)/-10*(x-13)/-11*(x-14)/-12*(x-15)/-13*(x-16)/-14*(x-17)/-15*(x-18)/-16*(x-19)/-17*(x-20)/-18*(x-21)/-19*(x-22)/-20*(x-23)/-21*(x-24)/-22*3+(x-0)/3*(x-1)/2*(x-2)/1*(x-4)/-1*(x-5)/-2*(x-6)/-3*(x-7)/-4*(x-8)/-5*(x-9)/-6*(x-10)/-7*(x-11)/-8*(x-12)/-9*(x-13)/-10*(x-14)/-11*(x-15)/-12*(x-16)/-13*(x-17)/-14*(x-18)/-15*(x-19)/-16*(x-20)/-17*(x-21)/-18*(x-22)/-19*(x-23)/-20*(x-24)/-21*4+(x-0)/4*(x-1)/3*(x-2)/2*(x-3)/1*(x-5)/-1*(x-6)/-2*(x-7)/-3*(x-8)/-4*(x-9)/-5*(x-10)/-6*(x-11)/-7*(x-12)/-8*(x-13)/-9*(x-14)/-10*(x-15)/-11*(x-16)/-12*(x-17)/-13*(x-18)/-14*(x-19)/-15*(x-20)/-16*(x-21)/-17*(x-22)/-18*(x-23)/-19*(x-24)/-20*5+(x-0)/5*(x-1)/4*(x-2)/3*(x-3)/2*(x-4)/1*(x-6)/-1*(x-7)/-2*(x-8)/-3*(x-9)/-4*(x-10)/-5*(x-11)/-6*(x-12)/-7*(x-13)/-8*(x-14)/-9*(x-15)/-10*(x-16)/-11*(x-17)/-12*(x-18)/-13*(x-19)/-14*(x-20)/-15*(x-21)/-16*(x-22)/-17*(x-23)/-18*(x-24)/-19*16+(x-0)/6*(x-1)/5*(x-2)/4*(x-3)/3*(x-4)/2*(x-5)/1*(x-7)/-1*(x-8)/-2*(x-9)/-3*(x-10)/-4*(x-11)/-5*(x-12)/-6*(x-13)/-7*(x-14)/-8*(x-15)/-9*(x-16)/-10*(x-17)/-11*(x-18)/-12*(x-19)/-13*(x-20)/-14*(x-21)/-15*(x-22)/-16*(x-23)/-17*(x-24)/-18*17+(x-0)/7*(x-1)/6*(x-2)/5*(x-3)/4*(x-4)/3*(x-5)/2*(x-6)/1*(x-8)/-1*(x-9)/-2*(x-10)/-3*(x-11)/-4*(x-12)/-5*(x-13)/-6*(x-14)/-7*(x-15)/-8*(x-16)/-9*(x-17)/-10*(x-18)/-11*(x-19)/-12*(x-20)/-13*(x-21)/-14*(x-22)/-15*(x-23)/-16*(x-24)/-17*18+(x-0)/8*(x-1)/7*(x-2)/6*(x-3)/5*(x-4)/4*(x-5)/3*(x-6)/2*(x-7)/1*(x-9)/-1*(x-10)/-2*(x-11)/-3*(x-12)/-4*(x-13)/-5*(x-14)/-6*(x-15)/-7*(x-16)/-8*(x-17)/-9*(x-18)/-10*(x-19)/-11*(x-20)/-12*(x-21)/-13*(x-22)/-14*(x-23)/-15*(x-24)/-16*19+(x-0)/9*(x-1)/8*(x-2)/7*(x-3)/6*(x-4)/5*(x-5)/4*(x-6)/3*(x-7)/2*(x-8)/1*(x-10)/-1*(x-11)/-2*(x-12)/-3*(x-13)/-4*(x-14)/-5*(x-15)/-6*(x-16)/-7*(x-17)/-8*(x-18)/-9*(x-19)/-10*(x-20)/-11*(x-21)/-12*(x-22)/-13*(x-23)/-14*(x-24)/-15*6+(x-0)/10*(x-1)/9*(x-2)/8*(x-3)/7*(x-4)/6*(x-5)/5*(x-6)/4*(x-7)/3*(x-8)/2*(x-9)/1*(x-11)/-1*(x-12)/-2*(x-13)/-3*(x-14)/-4*(x-15)/-5*(x-16)/-6*(x-17)/-7*(x-18)/-8*(x-19)/-9*(x-20)/-10*(x-21)/-11*(x-22)/-12*(x-23)/-13*(x-24)/-14*15+(x-0)/11*(x-1)/10*(x-2)/9*(x-3)/8*(x-4)/7*(x-5)/6*(x-6)/5*(x-7)/4*(x-8)/3*(x-9)/2*(x-10)/1*(x-12)/-1*(x-13)/-2*(x-14)/-3*(x-15)/-4*(x-16)/-5*(x-17)/-6*(x-18)/-7*(x-19)/-8*(x-20)/-9*(x-21)/-10*(x-22)/-11*(x-23)/-12*(x-24)/-13*24+(x-0)/12*(x-1)/11*(x-2)/10*(x-3)/9*(x-4)/8*(x-5)/7*(x-6)/6*(x-7)/5*(x-8)/4*(x-9)/3*(x-10)/2*(x-11)/1*(x-13)/-1*(x-14)/-2*(x-15)/-3*(x-16)/-4*(x-17)/-5*(x-18)/-6*(x-19)/-7*(x-20)/-8*(x-21)/-9*(x-22)/-10*(x-23)/-11*(x-24)/-12*25+(x-0)/13*(x-1)/12*(x-2)/11*(x-3)/10*(x-4)/9*(x-5)/8*(x-6)/7*(x-7)/6*(x-8)/5*(x-9)/4*(x-10)/3*(x-11)/2*(x-12)/1*(x-14)/-1*(x-15)/-2*(x-16)/-3*(x-17)/-4*(x-18)/-5*(x-19)/-6*(x-20)/-7*(x-21)/-8*(x-22)/-9*(x-23)/-10*(x-24)/-11*20+(x-0)/14*(x-1)/13*(x-2)/12*(x-3)/11*(x-4)/10*(x-5)/9*(x-6)/8*(x-7)/7*(x-8)/6*(x-9)/5*(x-10)/4*(x-11)/3*(x-12)/2*(x-13)/1*(x-15)/-1*(x-16)/-2*(x-17)/-3*(x-18)/-4*(x-19)/-5*(x-20)/-6*(x-21)/-7*(x-22)/-8*(x-23)/-9*(x-24)/-10*7+(x-0)/15*(x-1)/14*(x-2)/13*(x-3)/12*(x-4)/11*(x-5)/10*(x-6)/9*(x-7)/8*(x-8)/7*(x-9)/6*(x-10)/5*(x-11)/4*(x-12)/3*(x-13)/2*(x-14)/1*(x-16)/-1*(x-17)/-2*(x-18)/-3*(x-19)/-4*(x-20)/-5*(x-21)/-6*(x-22)/-7*(x-23)/-8*(x-24)/-9*14+(x-0)/16*(x-1)/15*(x-2)/14*(x-3)/13*(x-4)/12*(x-5)/11*(x-6)/10*(x-7)/9*(x-8)/8*(x-9)/7*(x-10)/6*(x-11)/5*(x-12)/4*(x-13)/3*(x-14)/2*(x-15)/1*(x-17)/-1*(x-18)/-2*(x-19)/-3*(x-20)/-4*(x-21)/-5*(x-22)/-6*(x-23)/-7*(x-24)/-8*23+(x-0)/17*(x-1)/16*(x-2)/15*(x-3)/14*(x-4)/13*(x-5)/12*(x-6)/11*(x-7)/10*(x-8)/9*(x-9)/8*(x-10)/7*(x-11)/6*(x-12)/5*(x-13)/4*(x-14)/3*(x-15)/2*(x-16)/1*(x-18)/-1*(x-19)/-2*(x-20)/-3*(x-21)/-4*(x-22)/-5*(x-23)/-6*(x-24)/-7*22+(x-0)/18*(x-1)/17*(x-2)/16*(x-3)/15*(x-4)/14*(x-5)/13*(x-6)/12*(x-7)/11*(x-8)/10*(x-9)/9*(x-10)/8*(x-11)/7*(x-12)/6*(x-13)/5*(x-14)/4*(x-15)/3*(x-16)/2*(x-17)/1*(x-19)/-1*(x-20)/-2*(x-21)/-3*(x-22)/-4*(x-23)/-5*(x-24)/-6*21+(x-0)/19*(x-1)/18*(x-2)/17*(x-3)/16*(x-4)/15*(x-5)/14*(x-6)/13*(x-7)/12*(x-8)/11*(x-9)/10*(x-10)/9*(x-11)/8*(x-12)/7*(x-13)/6*(x-14)/5*(x-15)/4*(x-16)/3*(x-17)/2*(x-18)/1*(x-20)/-1*(x-21)/-2*(x-22)/-3*(x-23)/-4*(x-24)/-5*8+(x-0)/20*(x-1)/19*(x-2)/18*(x-3)/17*(x-4)/16*(x-5)/15*(x-6)/14*(x-7)/13*(x-8)/12*(x-9)/11*(x-10)/10*(x-11)/9*(x-12)/8*(x-13)/7*(x-14)/6*(x-15)/5*(x-16)/4*(x-17)/3*(x-18)/2*(x-19)/1*(x-21)/-1*(x-22)/-2*(x-23)/-3*(x-24)/-4*13+(x-0)/21*(x-1)/20*(x-2)/19*(x-3)/18*(x-4)/17*(x-5)/16*(x-6)/15*(x-7)/14*(x-8)/13*(x-9)/12*(x-10)/11*(x-11)/10*(x-12)/9*(x-13)/8*(x-14)/7*(x-15)/6*(x-16)/5*(x-17)/4*(x-18)/3*(x-19)/2*(x-20)/1*(x-22)/-1*(x-23)/-2*(x-24)/-3*12+(x-0)/22*(x-1)/21*(x-2)/20*(x-3)/19*(x-4)/18*(x-5)/17*(x-6)/16*(x-7)/15*(x-8)/14*(x-9)/13*(x-10)/12*(x-11)/11*(x-12)/10*(x-13)/9*(x-14)/8*(x-15)/7*(x-16)/6*(x-17)/5*(x-18)/4*(x-19)/3*(x-20)/2*(x-21)/1*(x-23)/-1*(x-24)/-2*11+(x-0)/23*(x-1)/22*(x-2)/21*(x-3)/20*(x-4)/19*(x-5)/18*(x-6)/17*(x-7)/16*(x-8)/15*(x-9)/14*(x-10)/13*(x-11)/12*(x-12)/11*(x-13)/10*(x-14)/9*(x-15)/8*(x-16)/7*(x-17)/6*(x-18)/5*(x-19)/4*(x-20)/3*(x-21)/2*(x-22)/1*(x-24)/-1*10+(x-0)/24*(x-1)/23*(x-2)/22*(x-3)/21*(x-4)/20*(x-5)/19*(x-6)/18*(x-7)/17*(x-8)/16*(x-9)/15*(x-10)/14*(x-11)/13*(x-12)/12*(x-13)/11*(x-14)/10*(x-15)/9*(x-16)/8*(x-17)/7*(x-18)/6*(x-19)/5*(x-20)/4*(x-21)/3*(x-22)/2*(x-23)/1*9
이 함수의 그래프는 다음과 같다.
그림4. 5x5 달팽이 함수의 그래프
저걸 깔끔하게 정리하면 그림2에 나와있는 함수처럼 될것이다. 근데 길이만 봐도 알겠지만 항의 갯수가 엄청 많다. n by n 달팽이 함수를 만들기 위해서는 저 파이 옆에 있는 분수 모양을 n^4개 계산해야 한다. 저걸 손으로 계산하는건 별로 하고 싶지도 않고, 5x5 달팽이만을 위해 저 계산을 하긴 싫으니6 저 '함수' 를 만들어주는 프로그램을 만들기로 한다.
라그랑주 달팽이 행렬 제작기
함수를 만들어 주는 프로그램이라니. 뭔가 거창해 보이지만 별거 없다. N을 커맨드 라인 인자로 받아서 저 함수 수식 문자열을 출력하는 프로그램이면 충분하다. (저 위의 함수도 이 프로그램으로 만든것이다)
그림5. 애초에 이렇게 쓸 생각이었다. (파일로 출력하는 기능도 없어서 입출력 재지정을 사용한다)
함수의 y값들을 알아야 함수를 만들수 있기 때문에 일단 달팽이 배열을 만들어 놓는다. 이때 슬슬 졸리기 시작해서 비효율적이더라도 손 가는대로 짰다.
이제 y 값을 토대로 함수 내용을 만들어 바치기로 한다. 사실 여기도 별것없다. 위 식을 보고 시그마와 파이에 맞춰서 for문 중첩 해주고, 연산자와 값을 문자열 형태로 출력하면 된다. ('=' 부터 ';' 까지 출력한다)
전체 코드는 gist에. 예외처리는 최소한만 해 놓았다.
결과 값으로 나온 함수 수식을 다음과 같이 사용하면, 간단한 함수 하나로 달팽이 배열을 쉽게 출력 할 수 있다.
그림 6. 실행 시연
왜 라그랑주 보간
다른 보간법도 많은데 '왜 라그랑주 보간을 사용했냐?' 하면 나는 '디씨에서 저거 썼으니까' 라고 답변하겠다. '그럼 왜 디씨 글은 이걸 썼을까?' 라고 물었을때 추측해보자면 '모든 명시된 점을 하나의 수식으로 다 지나가는 함수를 만들기 위해' 일것 같다. 제일 만만한 선형 보간도 모든 명시된 점을 다 지나간다. 하지만 하나의 수식으로 지나가진 않겠고 함수에 이런저런 if-else 조건이 덕지덕지 붙을것이다. 이런식으로.
그림7. 수식부터가 안 이쁘다 이런건
그리고 그래프도 아까 그림3 마냥 각지게 나올것이다. 그것도 별로 이쁘진 않겠지.
사족
사실 막 고도로 어려운 수학이 필요하거나 구현에 엄청난 시간이 들어간다거나 하진 않지만, 보간법의 사용법를 너무 제한적으로 생각하고 있어서 오래 걸렸던거 같다.
그림8. 결과 파일들
그냥 생각없이 100x100의 함수식을 구해봤는데 수식을 담은 파일 크기만 442MB다.
- 저 글의 작성일이 07년인데 그때 나는 아직 고딩이 아니었다. 아마 누군가 예전 링크를 올렸고, 내가 거길 타고 들어간듯 싶다 [본문으로]
- 기억이 잘못된건지 정작 저 링크에는 그 댓글이 없다. 다른글을 봤나.. 아무튼 이때 '라그랑주 보간법'이라는게 있다는걸 처음 알았다. [본문으로]
- arr[i][j] 처럼 [본문으로]
- arr[i * n + j] 처럼 [본문으로]
- arr[i * n + j] = F(i * n + j); 처럼 [본문으로]
- 저 함수 하나는 5x5짜리 달팽이 하나만 만들 수 있다. 7x7 달팽이나, 10x10 달팽이 함수는 또 따로 구해야 한다. [본문으로]
'프로그래밍' 카테고리의 다른 글
| Cost Amortization (0) | 2016.10.30 |
|---|---|
| Advanced GIT 발표자료 (0) | 2016.08.13 |
| 쿼터뷰 좌표계를 직교 좌표계로 변환해서 현재 위치 타일 좌표 검사하기 (0) | 2015.01.27 |
| 알고스팟 weird 문제 (2) | 2015.01.24 |
| 알고스팟 Boggle 문제 (0) | 2015.01.24 |







